排序 - 桶排序(Bucket Sort)详解

1. 桶排序介绍

桶排序（Bucket Sort） 又称箱排序，是一种比较常用的排序算法。其算法原理是将数组分到有限数量的桶里，再对每个桶分别排好序（可以是递归使用桶排序，也可以是使用其他排序算法将每个桶分别排好序），最后一次将每个桶中排好序的数输出。

2. 桶排序算法

桶排序的思想就是把待排序的数尽量均匀地放到各个桶中，再对各个桶进行局部的排序，最后再按序将各个桶中的数输出，即可得到排好序的数。

1. 首先确定桶的个数。因为桶排序最好是将数据均匀地分散在各个桶中，那么桶的个数最好是应该根据数据的分散情况来确定。首先找出所有数据中的最大值mx和最小值mn；

   • 根据mx和mn确定每个桶所装的数据的范围 size，有size = (mx - mn) / n + 1，n为数据的个数，需要保证至少有一个桶，故而需要加个1；
   • 求得了size即知道了每个桶所装数据的范围，还需要计算出所需的桶的个数cnt，有cnt = (mx - mn) / size + 1，需要保证每个桶至少要能装1个数，故而需要加个1；

2. 求得了size和cnt后，即可知第一个桶装的数据范围为 [mn, mn + size)，第二个桶为 [mn + size, mn + 2 * size)，…，以此类推。因此步骤2中需要再扫描一遍数组，将待排序的各个数放进对应的桶中。

3. 对各个桶中的数据进行排序，可以使用其他的排序算法排序，例如快速排序；也可以递归使用桶排序进行排序；

4. 将各个桶中排好序的数据依次输出，最后得到的数据即为最终有序。

例子

例如，待排序的数为：3, 6, 9, 1

1. 求得 mx = 9，mn = 1，n = 4

size = （9 - 1) / n + 1 = 3
cnt = (mx - mn) / size + 1 = 3

2. 由上面的步骤可知，共3个桶，每个桶能放3个数，第一个桶数的范围为 [1, 4)，第二个[4, 7)，第三个[7, 10)。扫描一遍待排序的数，将各个数放到其对应的桶中，放完后如下图所示：

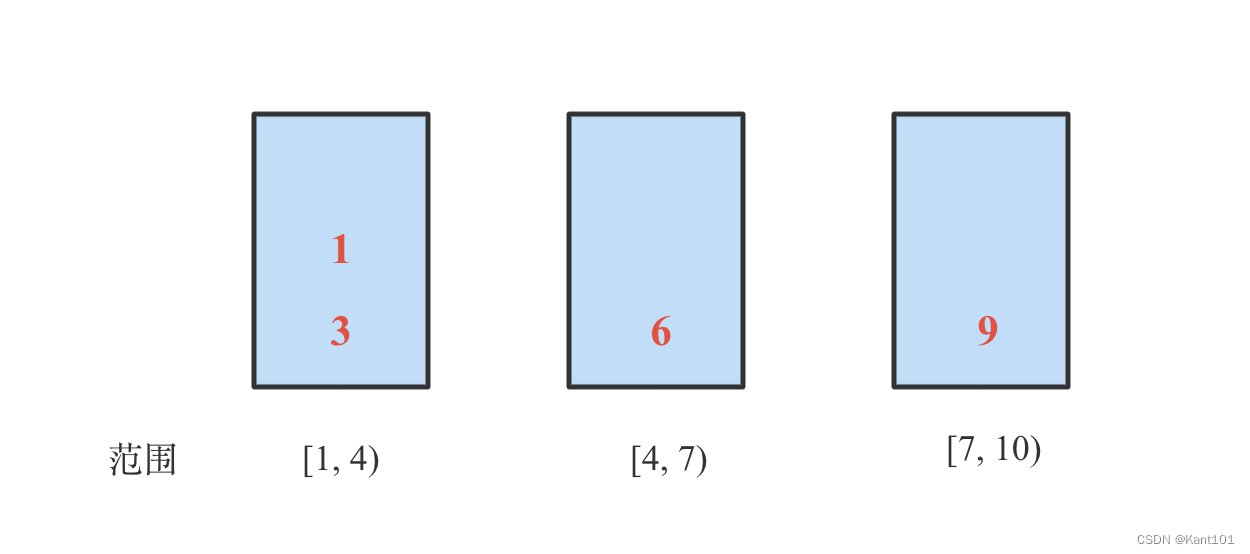
3. 对各个桶中的数进行排序，得到如下图所示：

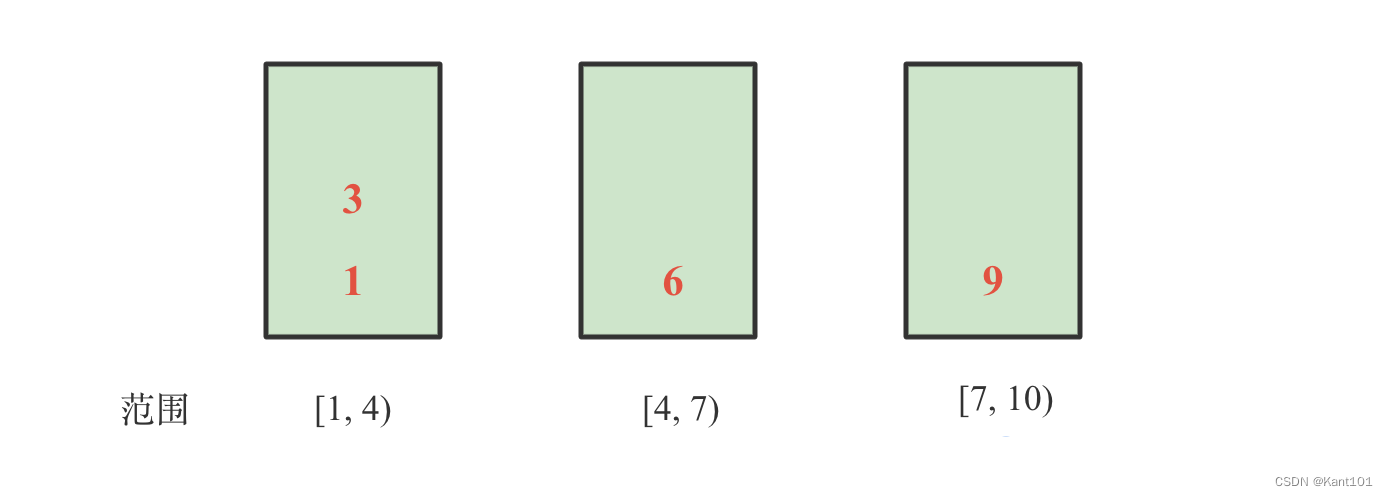
4. 依次输出各个排好序的桶中的数据，即为：1, 3, 6, 9。可见，最终得到了有序的排列。

3. 代码实现

3.1. 桶排序JAVA实现

实现代码(BucketSort.java)，如下：

import java.util.ArrayList;

/**
 * @author yumu
 * @date 2022/8/25
 */
public class BucketSort {

    public void bucketSort(int[] nums) {
        int n = nums.length;
        int mn = nums[0], mx = nums[0];
        // 找出数组中的最大最小值
        for (int i = 1; i < n; i++) {
            mn = Math.min(mn, nums[i]);
            mx = Math.max(mx, nums[i]);
        }
        int size = (mx - mn) / n + 1; // 每个桶存储数的范围大小，使得数尽量均匀地分布在各个桶中，保证最少存储一个
        int cnt = (mx - mn) / size + 1; // 桶的个数，保证桶的个数至少为1
        List<Integer>[] buckets = new List[cnt]; // 声明cnt个桶
        for (int i = 0; i < cnt; i++) {
            buckets[i] = new ArrayList<>();
        }
        // 扫描一遍数组，将数放进桶里
        for (int i = 0; i < n; i++) {
            int idx = (nums[i] - mn) / size;
            buckets[idx].add(nums[i]);
        }
        // 对各个桶中的数进行排序，这里用库函数快速排序
        for (int i = 0; i < cnt; i++) {
            buckets[i].sort(null); // 默认是按从小打到排序
        }
        // 依次将各个桶中的数据放入返回数组中
        int index = 0;
        for (int i = 0; i < cnt; i++) {
            for (int j = 0; j < buckets[i].size(); j++) {
                nums[index++] = buckets[i].get(j);
            }
        }
    }

    public static void main(String[] args) {
        int[] nums = {19, 27, 35, 43, 31, 22, 54, 66, 78};
        BucketSort bucketSort = new BucketSort();
        bucketSort.bucketSort(nums);
        for (int num: nums) {
            System.out.print(num + " ");
        }
        System.out.println();
    }
}

3.2. 桶排序C实现

实现代码(bucket_sort.c)，如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 数组长度
#define LENGTH(array) ( (sizeof(array)) / (sizeof(array[0])) )

void bucket_sort(int a[], int n, int max)
{
    int i, j;
    int *buckets;

    if (a==NULL || n<1 || max<1)
        return ;

    // 创建一个容量为max的数组buckets，并且将buckets中的所有数据都初始化为0。
    if ((buckets=(int *)malloc(max*sizeof(int)))==NULL)
        return ;
    memset(buckets, 0, max*sizeof(int));

    // 1. 计数
    for(i = 0; i < n; i++)
        buckets[a[i]]++;

    // 2. 排序
    for (i = 0, j = 0; i < max; i++)
        while( (buckets[i]--) >0 )
            a[j++] = i;

    free(buckets);
}

void main()
{
    int i;
    int a[] = {19, 27, 35, 43, 31, 22, 54, 66, 78};
    int ilen = LENGTH(a);

    printf("before sort:");
    for (i=0; i<ilen; i++)
        printf("%d ", a[i]);
    printf("\n");

    bucket_sort(a, ilen, 10); // 桶排序

    printf("after  sort:");
    for (i=0; i<ilen; i++)
        printf("%d ", a[i]);
    printf("\n");
}

3.3. 桶排序C++实现

实现代码(BucketSort.cpp)，如下：

#include <iostream>
#include <vector>

using namespace std;

class BucketSort {
public:
    void bucketSort(vector<int> &nums) {
        int n = nums.size();
        int mn = nums[0], mx = nums[0];
        for (int i = 1; i < n; i++) {
            mn = min(mn, nums[i]);
            mx = max(mx, nums[i]);
        }
        int size = (mx - mn) / n + 1;   // size 至少要为1
        int cnt = (mx - mn) / size + 1; // 桶的个数至少要为1
        vector<vector<int>> buckets(cnt);
        for (int i = 0; i < n; i++) {
            int idx = (nums[i] - mn) / size;
            buckets[idx].push_back(nums[i]);
        }
        for (int i = 0; i < cnt; i++) {
            sort(buckets[i].begin(), buckets[i].end());
        }
        int index = 0;
        for (int i = 0; i < cnt; i++) {
            for (int j = 0; j < buckets[i].size(); j++) {
                nums[index++] = buckets[i][j];
            }
        }
    }
};


int main() {
    vector<int> nums = {19, 27, 35, 43, 31, 22, 54, 66, 78};
    BucketSort().bucketSort(nums);
    for (auto num: nums) {
        cout << num << " ";
    }
    cout << endl;
    return 0;
}

上面3种实现的原理和输出结果都是一样的。下面是它们的输出结果：

before sort:19 27 35 43 31 22 54 66 78
after  sort:19 22 27 31 35 43 54 66 78

4. 时间和空间复杂度

最好时间复杂度 : O(n + k)

其中k为桶的个数。即当数据是均匀分散排列的，那么每个桶分到的数据个数都是一样的，这个步骤需要O(k)的书剑复杂度，在对每个桶进行排序的时候，最好情况下是数据都已经是有序的了，那么最好的排序算法的时间复杂度会是O(n)，因此总的时间复杂度是 O(n + k) 。

最坏时间复杂度：O(n^2)

当对每个桶中的数据进行排序的时候，所使用的排序算法，最坏情况下是O(n^{2)，因此总的最坏情况下的时间复杂度为O(n}2）。

平均时间复杂度：O(n + n²/k + k) <=> O(n)

如果k是根据Θ(n)来获取的，那么平均时间复杂度就是 O(n)。

引用资料

• https://blog.csdn.net/qq_27198345/article/details/126516234

手机看

微信扫一扫微信小程序：Java精选面试题，刷题，各种个性化功能！

交流圈

添加东哥微信进《程序员专属》学习交流圈「无任何套路」 PS：添加时请备注素文宅，谢谢！

下资料

扫描公众号，回复“资料”下载500GB+书籍资料「无任何套路」公众号：Java精选

支持我

赞赏/支持我莫愁前路无知己，天下谁人不识君！

--- 阅读全文-人机检测 ---

×

扫码关注公众号：Java精选
发送：yyds
获取永久解锁本站全部文章的验证码
注：微信搜索小程序“Java精选面试题”，内涵3000+道免费面试题，在线刷！